이 궁금증의 발단은 백준의 한 알고리즘 문제를 풀면서 시작됐다.
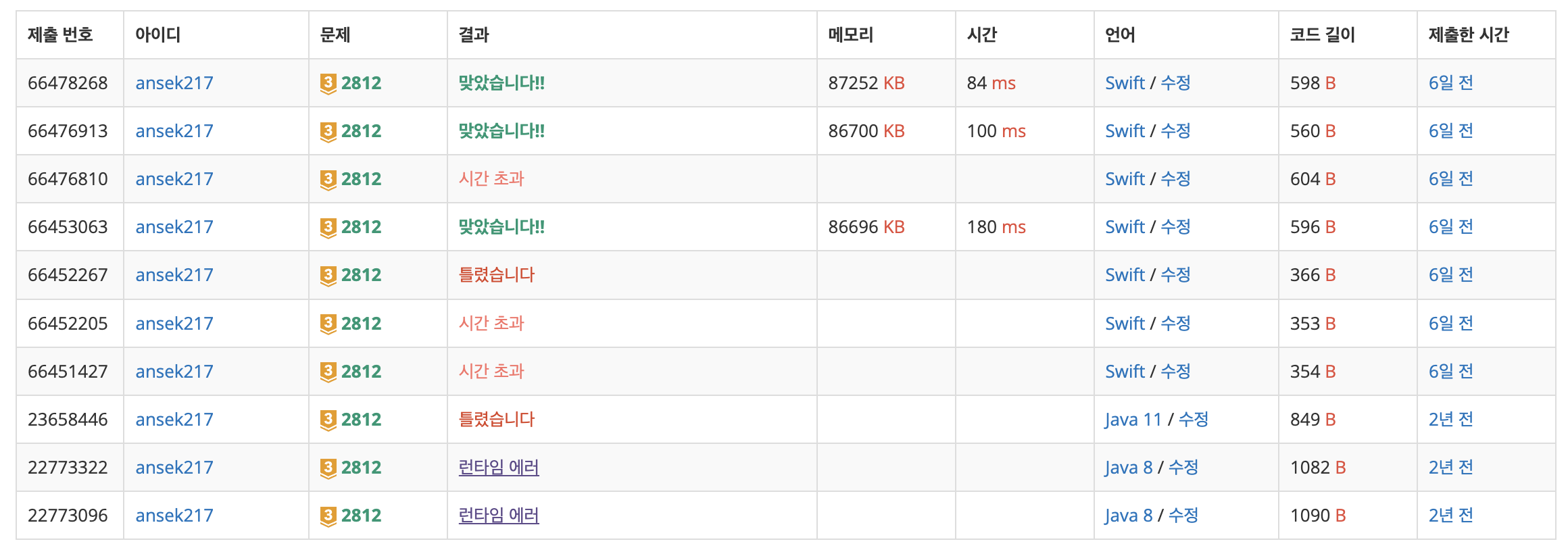
BOJ 2812번이다. 이 포스트에서 문제는 별로 중요하지 않아서 설명하지 않는다.
다만 문제를 해결하는 방식에서 [String 배열을 한 문자열로 합친다]를 코드로 작성해야 했다. 하...😂 평소같았으면 2번을 joined() 함수를 사용해서 한 문자열로 합쳐줘서 간단히 해결됐을 것 같은데, 머리를 너무 써서 더 바보같은 방법을 사용했다! 그건 바로 reduce()! 이미지에서 시간초과가 난 것들은 모두 reduce를 사용해준 풀이이다. 처음 맞았을 때는 joined()도 아니고 반복문을 돌려 print해서 맞춘거다. reduce도 O(n), for문도 O(n)이라 생각한 나는 믿기지 않아서 reduce 풀이로 다시 제출했다가 또 틀려줬음..ㅎㅋㅋㅋ

스터디때 답을 얻을 수 있을 것 같아서 질문을 만들어 갔다. 저때는 고차함수를 체이닝해서 사용해서 O(n^2)이 되는줄 알았다. 근데 체이닝하지 않고 각각 써주면 또 O(n)이 아닌가? 왜 reduce만 시간초과가 나는걸까? 공식문서를 먼저 살펴봤다.
reduce(_:_:)
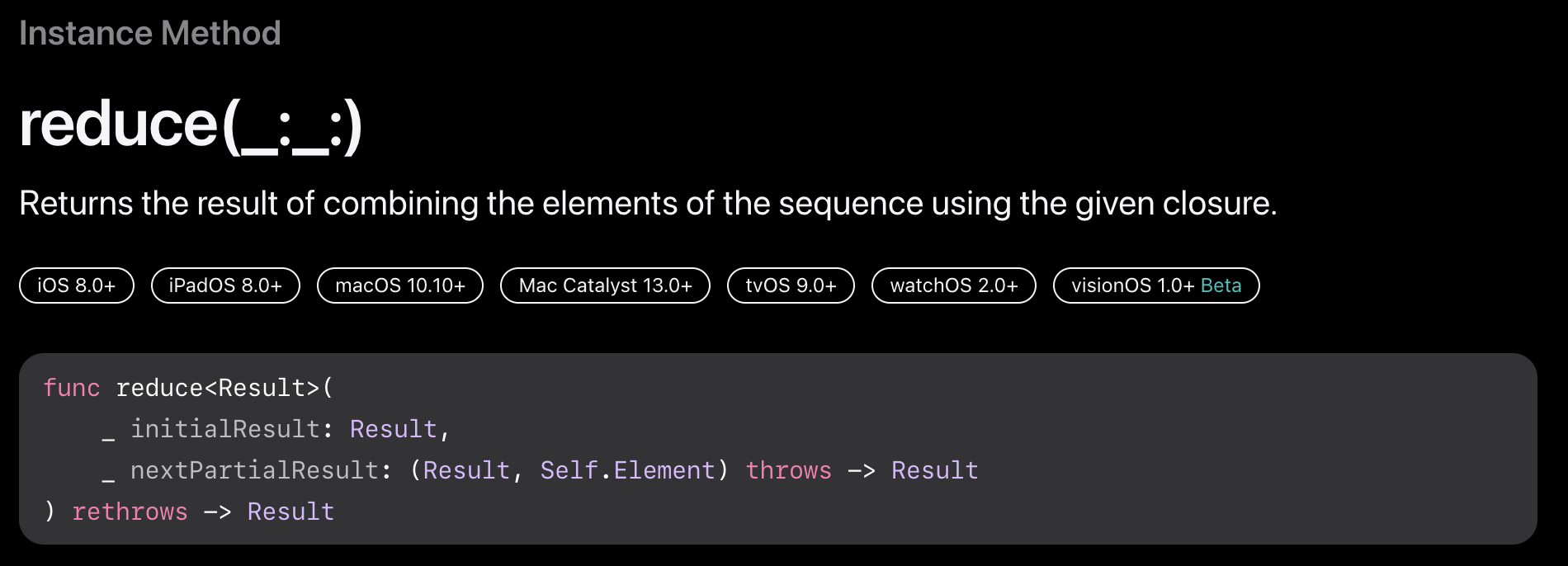
그러니까 전체 시퀀스의 요소들로부터 하나의 값을 생성해줄건데 그 값은 클로저에 따라 정해진다. 파라미터로 사용하는 initialResult는 초기값이며, nextPartialResult 클로저의 연산으로 시퀀스의 각 요소를 순차적으로 호출해 초기값에 누적하도록 한다.

그러니까 중요한건 시퀀스를 순차적으로 돌면서 하나씩 누적해간다. ....잉? 그니까 O(n)은 맞는 것 같다?... 일단 다음으로 joined()를 살펴보자.
joined(sparator:)
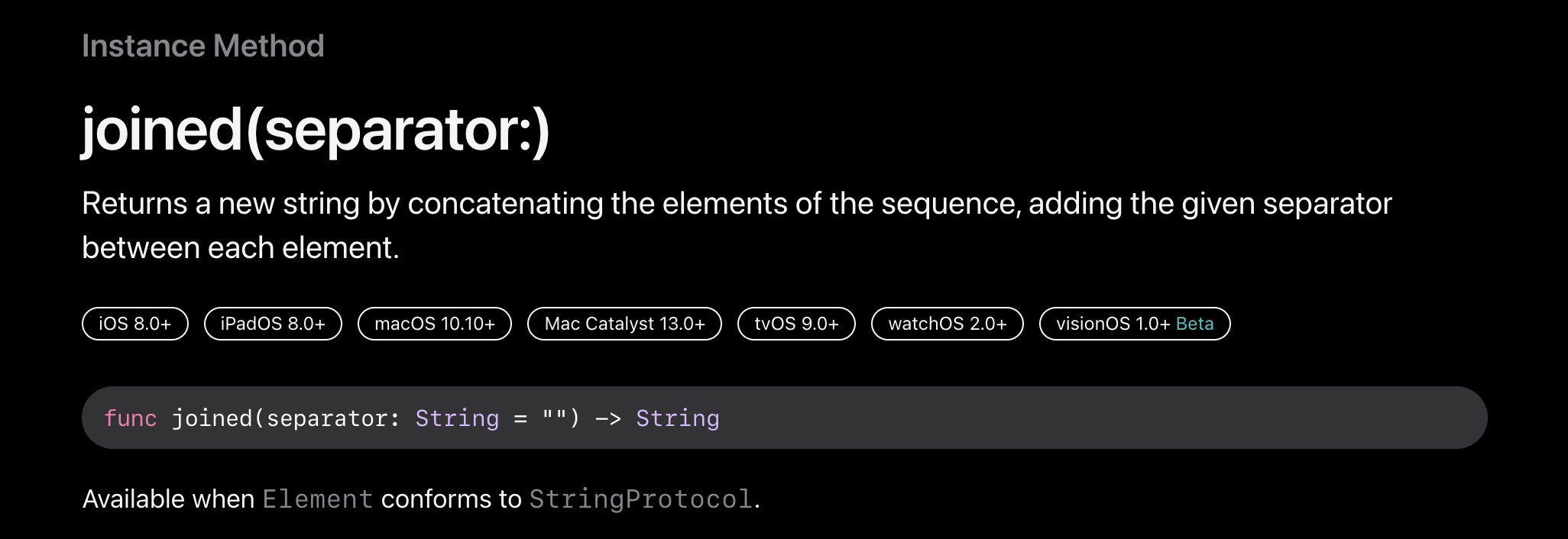
시퀀스의 요소를 연결하고 각 요소 사이에 seperator를 추가하여 새 문자열을 반환한다. 왜인지 joined()는 시간복잡도가 공식문서에서 명시되어 있지 않다. 하지만 결국 StringProtocol을 따르는 시퀀스 내 요소들을 하나씩 연결하고 중간에 separator를 추가해주는 것이기 때문에 추정컨대 O(n)일 것이다.
그럼 다시, 왜 reduce()만 시간초과가 발생할까?
이 알고리즘 문제의 제한시간은 1초이며, Character 배열을 String 이니셜라이저의 파라미터로 넣어 제출한 풀이가 정확히 0.1초였다. 이 문제를 해결할 수 있는건 joined 메소드뿐만 아니라 for문, String 이니셜라이저의 사용이다. 이 방법들의 공통점은 시간복잡도가 내가 생각하기에 확신의 O(n)이라는 것이다.
나는 이제야 여기서부터 슬슬 깨달았다. 가장 의심스러운 놈은 문자열 그 자체다. 스터디하면서도 스터디원 중 한명이 스위프트 String의 특수한 성질을 언급했었는데, 이때 뭐라고 검색했는지는 모르겠지만 지피티가 O(4n)이라고 대답해줬다고 아닌 것 같다고해서 예외 처리하고 있었다. 멍청피티
결론적으로는 이 부분이 문제였다. 드디어 "문자열을 더하는 연산(+)이 O(1)인가?"라는 질문을 생각해냈다. 그 대답은 아니다. 문자열의 더하기 연산은 두 문자열을 하나로 결합해야 하므로, 문자열의 길이가 길어질수록 시간이 비례적으로 증가한다. 따라서 길이가 n, m인 두 문자열을 더한다고 할 때, 이는 O(n+m)의 시간복잡도를 가진다고 한다. 참고로 정수형은 O(1)이 맞다.
그럼 append()는 어떨까? 기준 문자열이 있고, 추가되는 문자열의 수에 시간이 비례하기 때문에 평균적으로는 O(1)이지만, 너무 길면 최악의 경우 O(n)까지도 발생할 수 있다고 한다.
혼자 생각해보기에 이러한 차이가 발생하는 원인은 복사 작업 때문일 것 같다. [문자열 더하기(+) 연산]의 경우 두 문자열을 각각 복사해오기 때문에 두 문자열의 길이 합에 비례하고, [append]의 경우에는 기존 문자열에 파라미터로 받은 문자열을 추가하는 것이므로, 추가되는 문자열의 수에 비례할 것이다. 요런 너낌. 맞는지 모름.
백준에서는 reduce()의 클로저로 append 연산을 받도록 바꾸어 제출해봤는데도 시간초과가 발생했다. 문자에서 주어진 최대 문자열의 길이가 500,000인데, 예제 코드로 보니 문자열의 길이가 1,000만 넘어가도 더하기 연산과 실행시간이 비슷하더라.
실행시간을 두 눈으로 확인해보자 👀
합쳐야 하는 문자열의 크기는 최대값인 500,000으로 설정해 차이를 확실히 확인하고자 했따!
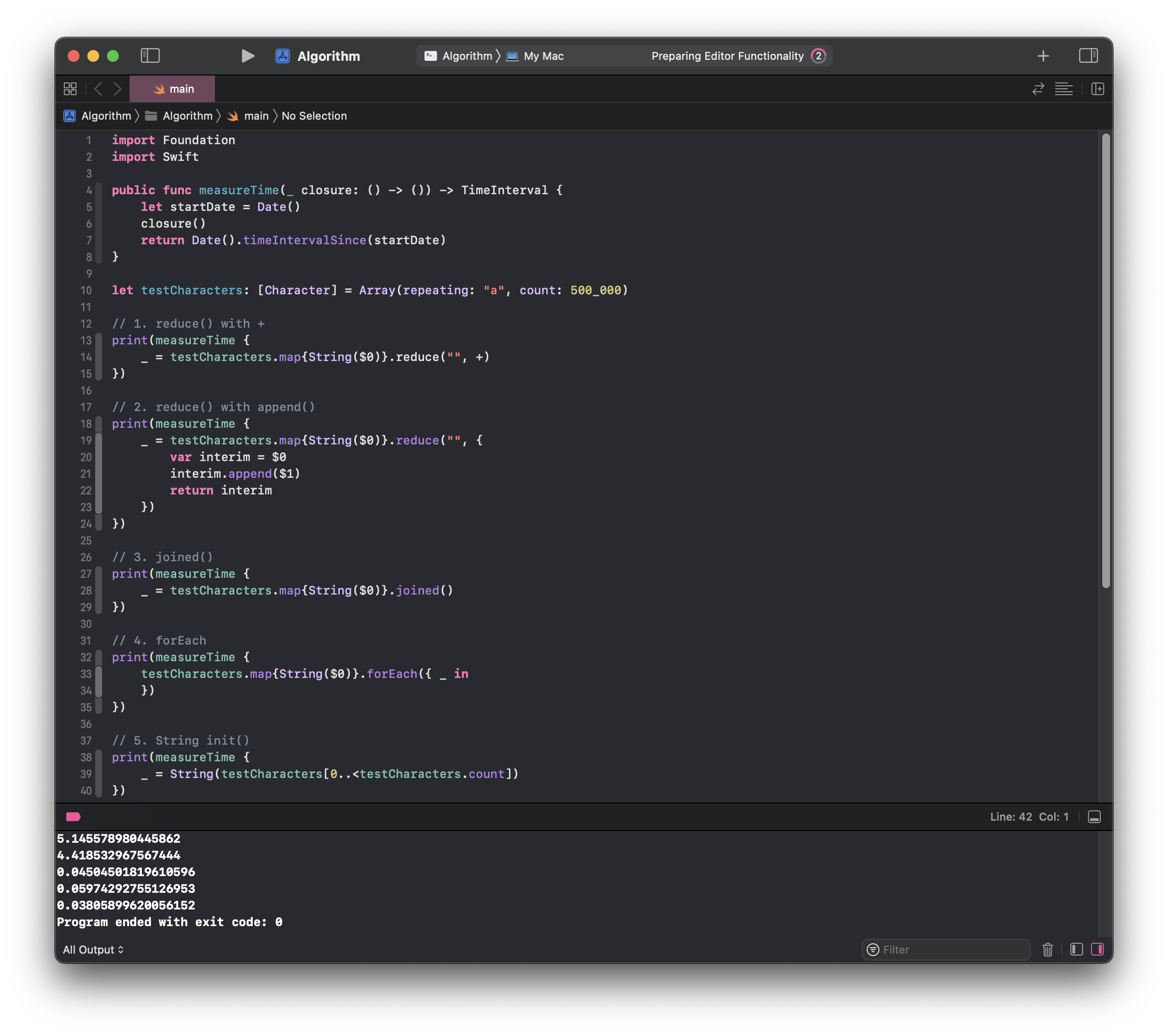
방금 언급했듯 문자열의 크기가 너무 커지면 append()도 O(n)의 시간복잡도를 갖게 되면서 1, 2번 방식 모두 O(n^2)의 시간 복잡도를 보인다.
3, 4, 5번은 O(n)의 시간 복잡도를 가진다. 3, 4번은 map()으로 한 번 거쳐서 시간이 조금 더 걸린데 반해 5번은 배열의 인덱스 접근으로 한 번만 순회하고 있어 3, 4번에 비해 5번이 조오오금 더 빠르다.
히유 결과적으로 시간복잡도가 O(n)인 reduce()의 클로저로 O(n) 연산을 해주었으니 O(n^2)이 된듯하다. 이 글의 제목을 쓸 땐 String의 joined와 reduce의 차이가 문제일거라 생각했는데, 결론적으로 시간초과의 원인은 String의 더하기 연산이었다. 너무 궁금했는데 지난 주에 명확한 답을 못찾고 답답했던 게 생각나서 정리해봤다. 안했으면 그냥 백준 서버 문제라고 생각하고 넘어갔을뻔 😮💨
끗 -
이 궁금증의 발단은 백준의 한 알고리즘 문제를 풀면서 시작됐다.

BOJ 2812번이다. 이 포스트에서 문제는 별로 중요하지 않아서 설명하지 않는다.
다만 문제를 해결하는 방식에서 [String 배열을 한 문자열로 합친다]를 코드로 작성해야 했다. 하...😂 평소같았으면 2번을 joined() 함수를 사용해서 한 문자열로 합쳐줘서 간단히 해결됐을 것 같은데, 머리를 너무 써서 더 바보같은 방법을 사용했다! 그건 바로 reduce()! 이미지에서 시간초과가 난 것들은 모두 reduce를 사용해준 풀이이다. 처음 맞았을 때는 joined()도 아니고 반복문을 돌려 print해서 맞춘거다. reduce도 O(n), for문도 O(n)이라 생각한 나는 믿기지 않아서 reduce 풀이로 다시 제출했다가 또 틀려줬음..ㅎㅋㅋㅋ

스터디때 답을 얻을 수 있을 것 같아서 질문을 만들어 갔다. 저때는 고차함수를 체이닝해서 사용해서 O(n^2)이 되는줄 알았다. 근데 체이닝하지 않고 각각 써주면 또 O(n)이 아닌가? 왜 reduce만 시간초과가 나는걸까? 공식문서를 먼저 살펴봤다.
reduce(_:_:)

그러니까 전체 시퀀스의 요소들로부터 하나의 값을 생성해줄건데 그 값은 클로저에 따라 정해진다. 파라미터로 사용하는 initialResult는 초기값이며, nextPartialResult 클로저의 연산으로 시퀀스의 각 요소를 순차적으로 호출해 초기값에 누적하도록 한다.

그러니까 중요한건 시퀀스를 순차적으로 돌면서 하나씩 누적해간다. ....잉? 그니까 O(n)은 맞는 것 같다?... 일단 다음으로 joined()를 살펴보자.
joined(sparator:)

시퀀스의 요소를 연결하고 각 요소 사이에 seperator를 추가하여 새 문자열을 반환한다. 왜인지 joined()는 시간복잡도가 공식문서에서 명시되어 있지 않다. 하지만 결국 StringProtocol을 따르는 시퀀스 내 요소들을 하나씩 연결하고 중간에 separator를 추가해주는 것이기 때문에 추정컨대 O(n)일 것이다.
그럼 다시, 왜 reduce()만 시간초과가 발생할까?
이 알고리즘 문제의 제한시간은 1초이며, Character 배열을 String 이니셜라이저의 파라미터로 넣어 제출한 풀이가 정확히 0.1초였다. 이 문제를 해결할 수 있는건 joined 메소드뿐만 아니라 for문, String 이니셜라이저의 사용이다. 이 방법들의 공통점은 시간복잡도가 내가 생각하기에 확신의 O(n)이라는 것이다.
나는 이제야 여기서부터 슬슬 깨달았다. 가장 의심스러운 놈은 문자열 그 자체다. 스터디하면서도 스터디원 중 한명이 스위프트 String의 특수한 성질을 언급했었는데, 이때 뭐라고 검색했는지는 모르겠지만 지피티가 O(4n)이라고 대답해줬다고 아닌 것 같다고해서 예외 처리하고 있었다. 멍청피티
결론적으로는 이 부분이 문제였다. 드디어 "문자열을 더하는 연산(+)이 O(1)인가?"라는 질문을 생각해냈다. 그 대답은 아니다. 문자열의 더하기 연산은 두 문자열을 하나로 결합해야 하므로, 문자열의 길이가 길어질수록 시간이 비례적으로 증가한다. 따라서 길이가 n, m인 두 문자열을 더한다고 할 때, 이는 O(n+m)의 시간복잡도를 가진다고 한다. 참고로 정수형은 O(1)이 맞다.
그럼 append()는 어떨까? 기준 문자열이 있고, 추가되는 문자열의 수에 시간이 비례하기 때문에 평균적으로는 O(1)이지만, 너무 길면 최악의 경우 O(n)까지도 발생할 수 있다고 한다.
혼자 생각해보기에 이러한 차이가 발생하는 원인은 복사 작업 때문일 것 같다. [문자열 더하기(+) 연산]의 경우 두 문자열을 각각 복사해오기 때문에 두 문자열의 길이 합에 비례하고, [append]의 경우에는 기존 문자열에 파라미터로 받은 문자열을 추가하는 것이므로, 추가되는 문자열의 수에 비례할 것이다. 요런 너낌. 맞는지 모름.
백준에서는 reduce()의 클로저로 append 연산을 받도록 바꾸어 제출해봤는데도 시간초과가 발생했다. 문자에서 주어진 최대 문자열의 길이가 500,000인데, 예제 코드로 보니 문자열의 길이가 1,000만 넘어가도 더하기 연산과 실행시간이 비슷하더라.
실행시간을 두 눈으로 확인해보자 👀
합쳐야 하는 문자열의 크기는 최대값인 500,000으로 설정해 차이를 확실히 확인하고자 했따!

방금 언급했듯 문자열의 크기가 너무 커지면 append()도 O(n)의 시간복잡도를 갖게 되면서 1, 2번 방식 모두 O(n^2)의 시간 복잡도를 보인다.
3, 4, 5번은 O(n)의 시간 복잡도를 가진다. 3, 4번은 map()으로 한 번 거쳐서 시간이 조금 더 걸린데 반해 5번은 배열의 인덱스 접근으로 한 번만 순회하고 있어 3, 4번에 비해 5번이 조오오금 더 빠르다.
히유 결과적으로 시간복잡도가 O(n)인 reduce()의 클로저로 O(n) 연산을 해주었으니 O(n^2)이 된듯하다. 이 글의 제목을 쓸 땐 String의 joined와 reduce의 차이가 문제일거라 생각했는데, 결론적으로 시간초과의 원인은 String의 더하기 연산이었다. 너무 궁금했는데 지난 주에 명확한 답을 못찾고 답답했던 게 생각나서 정리해봤다. 안했으면 그냥 백준 서버 문제라고 생각하고 넘어갔을뻔 😮💨
끗 -
